2/25/2018 Y2Y O-Champ in Mong Tseng Wai (Farsta courses for the elite classes)

On 2/25/2018, there was a one-person orienteering relay in Mong Tseng Wai, which is NW of Tin Shui Wai in Hong Kong. Before the race, we only knew that: 1) there were 3 maps for man elite (ME); 2) the race was a mass start; 3) each competitor had different route combinations, but all competitors would complete all the courses in the maps; and 4) the length of the race.

I immediately believed that the course would be in a Farsta format. After the race, I found that my guess was correct.

What is a Farsta course?

Farsta is one of the ways to branch a one-person relay course so that competitors can start together, but they cannot always follow from one another because each competitor runs a different combinations of branches.

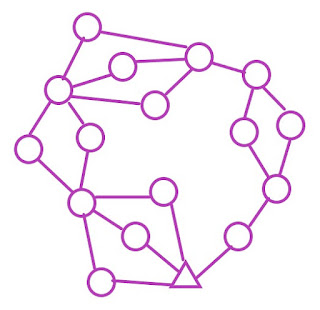
In a Farsta course, each map is divided into several segments, and each segment has several branches. If there are 3 maps, there will be no more than 3 branches. Each end of the segment has a node, where each branch leads to the same node. See the figure below.

In the figure above, there are 4 segments. Each segment contains 2 or 3 branches with one control point for each. Then, each branch meets at the same point.

In a map, one of the branches will be randomly given (e.g., 1A, 1B, or 1C). Then, the branches lead to the same node point (e.g., 2). Then, another one of the branches will be randomly given (e.g., 3A, or 3B), which leads to the same node point (e.g., 4), and so on. In the next map, another branch that is not completed yet will be given. At the end of running all maps, all the branches will be run through.

Note that in each branch, there can be more than one control. Moreover, some branches can be longer than the others. Normally, if there are 3 maps, there will be several segments with 3 branches each.

It is possible to follow the others under the Farsta format, but the competitors need to guess where the nodes are, in order to know whether they should continue to follow the same person or not. A possible hint is to see if there are people approaching the same control in different directions. Moreover, in the second map or after, the competitor should know where the nodes are by noticing the repeating controls.

One of the reasons that this one-person relay is called Farsta is that some common course setting software (e.g., Condes) puts the name Farsta as one of the options for overprinting course info on the map. Thus, setting Farsta course using software is not difficult.

The Setup of Farsta course in Mong Tseng Wai

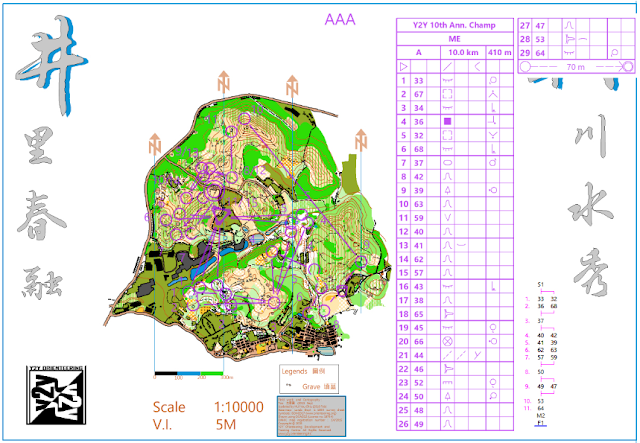
The map below shows the Farsta course, as a master map, that was done in Mong Tseng Wai:

In the above course, there are 3 segments with 3 branches each. There are 2 controls in each branch of the first segment, 1 control in each branch of the last segment. The number of controls in each branch of the middle segment varies. The nodes are control #37, #50, #53, and #64. Note that #53 and #64 are placed in the end of each course, probably so that all competitors will run the same route to the map changing area, and so that the spectators can see when each competitor finishes a map.

The following three maps show my branches:

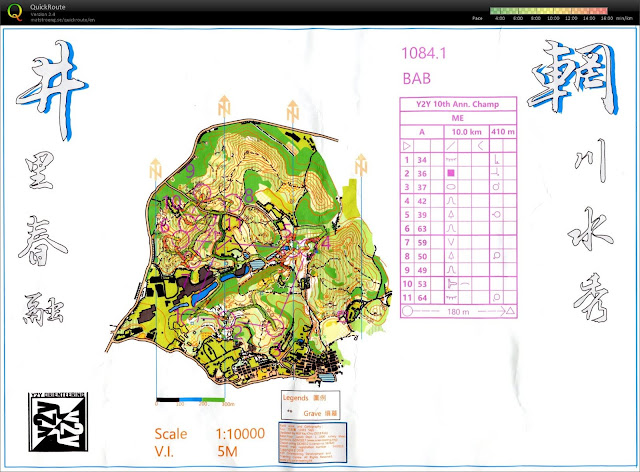
Map 1

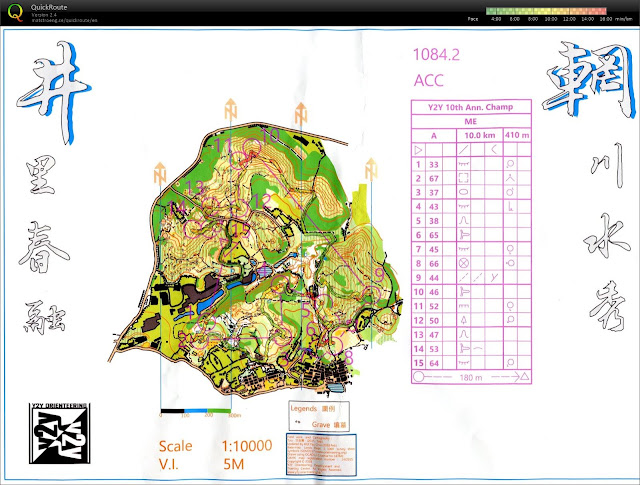
Map 2:

Map 3:

Each map has three letters on it. For example, in Map 1, it has BAB. This means the first segment is on Branch B, the second segment is on Branch A, and the third segment is on Branch B. It may not be useful for the competitors during the race, but the letters can be used to compare the legs when the competitors want to discuss them after the race -- find the map with the same segment and same branch, and then talk about it.

For those who are interested in math concerning counting, there is a general formula to calculate how many map combinations are available, if we know the number of segments (say m), and the number of branches and maps (say n), given that each segment has the same number of branches. The number is:

(n!)^m

For 3 segments with 3 branches each, there are 216 combinations.

Below is a nerdy explanation of the above formula, so you may skip to "post-race comments" unless you really want to know about why.

In each segment, the first map has n branches, so there is n possibilities. In the second map, one branch was chosen, so the second map has (n-1) possibilities. Similarly, the third map has (n-2) possibilities, and so on. This explains n! (= n(n-1)(n-2)...(1))

When adding another segment on a segment, a branch on one of the segments is independently connected to a branch of another segment. Thus, numbers of combinations for the two segments are multiplied to each other. This explains the ^m term. 

Post-race comments

It is a nice course. I just made too many mistakes on Map 1. When I want to the map exchange area, I saw only 3 other people not taking Map 2 yet. I think I did much better on Map 2 and 3.

The three branched controls in the third segment were very close to each other. It is easy to visit the other one if the map is not read carefully.

This is the first time to know that my SI card (the device that collects my control punching sequence) can only store 30 controls. In Map 3, I began to not hear beep at the control unit 41 (my 5th control). Thinking the unit may be malfunctioned, I used the spare mechanical punch to punch on the map (you can see the punch holes on Map 3 above). When I went to the next control, I could not hear beep either. I began to realize that it might be my SI card problem, so I used the mechanical punches all the way to the end. Fortunately, the results of my race got accepted. I was the only one who had this problem, since I used an older version of the SI card (SI-8). It is interesting to see that after I bought this for more than 7 years, this was the first time that I encountered the card memory problem in an orienteering race.

The organizer told me that it was time to replace the SI card. The new SI card can store more than 100 control numbers. If someone can tell me whether I can upgrade my SI card and how, it will be appreciated!